Author: Christopher Portmann

‍

‍

tl;dr Concordium’s voting protocol provides privacy and end-to-end verifiability. This article reviews what those terms mean and how homomorphic encryption and zero-knowledge proofs allow those security properties to be achieved in our blockchain elections. Our implementation of the protocol is open-source, and can be found on Concordium’s github repository.

The Importance of Privacy and Verifiability in Voting

In June 2024, Concordium will hold elections to add two members of the community to the Concordium governance committee. While many blockchains organize unencrypted on-chain elections, where everyone can see how everyone else voted, Concordium has chosen to use a state-of-the-art voting protocol that guarantees privacy of the votes. More generally, privacy requires that the (details of) transactions and accounts cannot be traced back to the account owners. But the pseudonymity typically provided by blockchains — i.e., transactions are public and tied to accounts, but accounts cannot be mapped to users — does not provide any true form of privacy, since blockchain forensics tools, on-chain analysis and linking with off-chain data can be used to identify account owners. Instead, one typically encrypts (parts of) transactions and account information (such as the balance) so that this information cannot be linked to the owner. In the context of elections, it should not be possible to know what vote was cast from what account, but one can usually know if an account voted or not. This is achieved by encrypting the vote before casting it.

The choice of holding elections with privacy was made because otherwise the elections are not free: if a person’s vote is public knowledge, this person is not free to vote as they want. This is particularly important in the context of elections to a governance body, since when elected members can see who voted for them and who didn’t, it can create (unconscious) biases that favor (the projects of) people who voted for the candidate.

Naturally, privacy alone is not sufficient. A user must also be certain that their vote was counted and that the result was correctly tallied. For a voting scheme that does not have privacy, this can be trivial: since all the votes are public, anyone can add them up to make sure that the result is correct. But if the votes are encrypted to preserve privacy, then proving that the result is correct without revealing how people voted is trickier. In the next sections, we will discuss the details of how Concordium’s voting system provides end-to-end verifiability. In a nutshell, zero-knowledge proofs are generated to prove that every step of the protocol was correctly executed. And since all ballots and all zero-knowledge proofs are put on-chain, they cannot be tampered with. So at any point in the future, an auditor with the knowledge to verify zero-knowledge proofs can verify that the voting protocol was correctly executed.

In the era of blockchains and zero-knowledge proofs, we have all the technical tools to organize free and fair elections. There is no excuse not to do so. Since the Concordium software is provided under the standard Apache License 2.0, anyone is welcome to reuse our code to organize secure (blockchain) voting of their own.

The rest of this article has two sections. In the section ‘The Voting Protocol’, we describe the voting protocol that we implemented for our blockchain elections, and in the section ‘Security Properties’ we review its security properties and how they are achieved.

The Voting Protocol

The voting protocol that we implemented is based on a partial implementation by Microsoft of a Rust version of their ElectionGuard v2.0 protocol. The source code of the protocol can be found in this github repository. The code for the integration with the Concordium blockchain is available in a different repository.

This section reviews the voting protocol. A reader interested in more technical details can read the Microsoft specification.

Encrypting and Tallying Weighted Votes

As mentioned in the first section, votes are encrypted to provide privacy. More specifically, a public key is generated and provided to all voters, who use it to encrypt their vote before casting it, i.e., before sending their ballot to the voting smart contract. Exactly how this key is generated and who holds the decryption keys is discussed in the next section, ‘Handling Secret Keys’.

There are many different voting systems. For example, a vote might designate one candidate or rank all candidates. We chose approval voting (see this article for more details on our election rules), where the voter gives either 0 or 1 to every candidate. So for the rest of this article, we will assume that a valid vote is v = 0 or v = 1, and that a vote is cast for every candidate.

Once all the votes for all the candidates have been encrypted and posted on the blockchain, we need to find a way to add them up without violating privacy, to determine how many votes every candidate received. There are different techniques used by e-voting protocols to do this. One complication in our setting is that for the Concordium election, we will not just add the votes

we weigh them by the amount of CCD — the token native to the Concordium blockchain — on every account, i.e., we need to determine the weighted sum

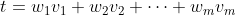
for every candidate, where w is the weight of the account that cast v.

Techniques that consist of anonymizing the votes by shuffling them and tallying them in plain do not work with weights: if a pair (w,v) is publicly visible, then information about the voter is leaked, because the weight w could allow the account to be identified — or at least, to drastically reduce the number of possible accounts that cast the vote v.

To tally the votes with weights, we use a special encryption scheme that has a property known as homomorphic addition, i.e., we can combine two ciphertexts together to get an encryption of the sum of the plaintext:

For our implementation, we use ElGamal with the message in the exponent.

For standard voting without weights, the voting protocol would add up all the votes for every candidate, obtaining the encrypted tally

One can then decrypt enc(t) and get the total number of votes for every candidate without revealing each vote.

Adding weights works particularly well with homomorphic encryption, because by combining a ciphertext w times with itself, we multiply the underlying plaintext by w, i.e.,

So the encrypted sum of the weighted votes can be computed as

This can easily be done, since for every encrypted vote enc(v) cast, we see from which account it was sent, so we know which weight w to apply.

There is still one major problem with the voting protocol presented so far: instead of encrypting 0 or 1, a voter could cast a ballot which contains the encryption of another number, e.g., 200. If we run the tallying protocol described above, then this voter will have given 200 votes to one of the candidates. To prevent this from happening, a voter must submit a zero-knowledge proof that their ciphertext is an encryption of either 0 or 1. And before tallying, we verify all zero-knowledge proofs and discard the votes that do not pass. All zero-knowledge proofs required by this protocol can be generated using standard techniques such as a sigma-protocol with the Fiat-Shamir transform, so we will not expand further on this.

Handling Secret Keys

The subsection ‘Encrypting and Tallying Weighted Votes’ above glosses over how the encryption key is generated and who holds the decryption key. If we were to have a single party generate the pair (pk,sk), distribute the public encryption key pk, keep the secret decryption key sk, and use sk to decrypt the tally t at the end of the protocol, then this party could use the same key sk to read every single vote and thus violate the voters’ privacy.

The solution is to have a decentralized voting committee that splits the secret key sk among the members using a secret sharing algorithm. Borrowing the terminology from Microsoft’s ElectionGuard, we call these committee members guardians. Secret sharing works as follows. We pick a polynomial p of degree d such that p(0) = sk, and send the point p(j) on the polynomial to guardian j. If at least d + 1 of the guardians work together, they have enough information to determine the secret (sk in our case), because d + 1 points are enough to interpolate. But any set of d or less guardians has no information about the secret.

We call such a secret sharing scheme a k-out-of-n threshold scheme if at least k guardians need to collaborate to recover the secret, i.e., the degree of the polynomial is d = k - 1. This means that as long as at most k - 1 guardians are corrupt, privacy is guaranteed, since there are not enough corrupt guardians to decrypt the individual votes. The protocol can also tolerate n - k guardians being absent, and it still has enough people to perform the decryption.

For our implementation, we will randomly choose community members to be the guardians. With a committee of size n = 11 and setting k = 6, privacy is guaranteed as long as at most 5 guardians are corrupt and the tally can be computed as long as at most 5 guardians do not run the correct protocol.

A somewhat simplified version of the key generation algorithm is as follows:

• Every guardian j generates a public and secret key pair (pk, sk). All the pk are published and the product of these keys is used as the encryption key by the voters. The secret key sk is the corresponding decryption key, but it is never computed explicitly, where

• Every guardian j secret shares their secret key with the other guardians, and proves in zero-knowledge that they did this step correctly. In case a proof does not verify, the faulty guardian can be excluded, and key generation restarts.
• Every guardian l sums the shares that they received, to get a value

• The sk’ form a k-out-of-n secret share of sk, and will be used during the decryption phase.

Proof of Correctness

The final step of the voting protocol is to perform the decryption of the tally. Since every guardian has a share of the secret key, every guardian can perform a decryption locally and obtain a share of the tally. We then interpolate between the tally shares to recover the tally. Note that since we use ElGamal with the message in the exponent, this last step involves computing a discrete logarithm to get the message. This is feasible if the space of possible messages is not too large (around 10 to the power 10 in our case, which is the total amount of CCD minted so far).

To prove that the tally is correct, every guardian needs to provide a zero-knowledge proof that they performed the decryption correctly. If at least k correct proofs are provided, then the result is guaranteed to correspond to the sum of the votes.

Security Properties

Privacy

Privacy of the individual votes holds under the assumption that at most k - 1 out of n guardians are corrupt and willing to work together to decrypt the individual votes. While we could set k = n and thus having one honest guardian is sufficient for privacy to hold, this would mean a single guardian not turning up for decryption would be enough not to be able to compute the tally — this is discussed further in the subsection ‘Robustness’ below. For our elections, we set k = 6 for n = 11 to balance privacy and robustness.

There exist voting protocols for which privacy holds no matter how many parties are corrupt, so-called self-tallying voting protocols. But they require every single voter to be part of the decentralized voting committee, which is infeasible in our setting, where a voter should be able to cast their vote in a minute from their cell phone, and not need to be active again after. Requiring a threshold of guardians to be honest for privacy to hold is the best that can be done in this setting.

We note that ElGamal is not quantum-safe. This means that when the development of quantum computers has reached the point where they can compute large discrete logarithms, it will be possible to decrypt the ballots produced today and find out how each individual account voted. The same also holds for improvements in classical computing.

Furthermore, simply publishing the result of a weighted vote can reveal some information about how individuals voted. This is not a vulnerability of the protocol, as it also happens in an ideal world where a trusted party gathers all the votes, tallies them and publishes the result. For example, if a voter has a lot of weight, then by looking at the tally we can know that they did not vote for any candidate whose total votes are less than this voter’s weight.

End-To-End Verifiability

Verifiability is the ability to check that the outcome of the e-voting protocol is correct. End-to-End verifiability can be broken down into three distinct parts.

Cast as intended. This means that if a voter selects candidate A on their interface, a ballot that encrypts a vote for A should be cast. Since our code is open source, auditors can verify that it is correct. There is also no requirement to use our implementation. The voting smart contract will accept any ballot satisfying the specification. This is arguably the weakest element in the verifiability chain of our implementation. There exist certain mitigation techniques such as casting test votes which are then opened to prove that the software correctly encrypts the ballots, and which might be implemented for future elections.

Recorded as cast. This means that all ballots cast by legitimate voters and only ballots cast by legitimate voters are recorded. In our implementation, this follows directly from the use of a blockchain as a bulletin board. Protocols that use simpler implementations of a bulletin board often require a trusted authority to sign off on the list of ballots. A blockchain essentially decentralizes this authority. So security of this part holds under the same conditions as the security of the blockchain: to guarantee that all ballots cast are recorded, we need at least 2/3 of the validators weighted by stake to be honest and the network conditions must allow all sent ballots to arrive.

Tallied as recorded. This final step guarantees that all valid votes recorded (and only valid votes) are correctly tallied. This part follows from the extensive use of zero-knowledge proofs throughout the protocol. Firstly, during key generation the guardians need to prove that they know the secret key corresponding to their public key and that they correctly shared it with the other guardians. This guarantees that any decryption performed with a sufficient number of honest guardians will produce the right outcome. Secondly, when generating ballots, the software also generates a proof that the ballot encrypts a valid vote. Authentication of the voter is taken care of on the layer of the blockchain. So only valid votes from account holders will be tallied. And thirdly, the guardians need to prove during the tally phase that they performed the decryption correctly. If all these zero-knowledge proofs are valid, then we have the guarantee that the final tally is correct.

In summary, an auditor who wants to verify the election results needs to check:

• That all zero-knowledge proofs generated by the guardians during the key set-up phase are valid.
• That the public key was correctly computed from the individual parts.
• That the encryption software correctly encrypts the votes.
• That the weights of all accounts were correctly calculated.
• That all ballots on the chain with valid zero-knowledge proofs were correctly aggregated with the corresponding weights.
• That the decryption zero-knowledge proof is valid.

If all these steps verify, if 2/3 of the blockchain validators weighted by stake are honest, and if the network conditions allow all sent ballots to arrive, then we have the guarantee that any tally obtained from the e-voting protocol is correct.

Robustness

As stated at the end of the previous subsection, if a tally is obtained, then it is guaranteed to be correct. But it is possible for the e-voting protocol to not produce a tally. This can happen if not enough guardians correctly execute the decryption phase. As stated in the subsection ‘Privacy’, there is a tradeoff between privacy and robustness. Let p denote the maximum number of corrupt parties that can be tolerated and still have privacy, and let r denote the maximum number of corrupt parties that can be tolerated and still have robustness. We necessarily have

where n is the total number of guardians. For n = 11 we chose p = r = 5, so our protocol can tolerate 5 faulty guardians and still produce an outcome.

Adding this to the list of requirements, we find that the voting protocol will produce the correct outcome with privacy if:

• 2/3 of the blockchain validators weighted by stake are honest,
• the network conditions allow all sent ballots to arrive,
• the list of bullet points in the subsection ‘End-To-End Verifiability’ (in particular, all zero-knowledge proofs) all verify,
• at most 5 out of 11 guardians are dishonest or absent.

For more information about Concordium’s 2024 governance committee election see:

• Concordium Governance Committee Election Rules 2024
• Governance Decentralization: Introducing the first Election for Concordium’s Governance Committee in 2024

‍